|  |  |  |  |
|  |  |  |  |  | |  |  |  |  |  | | Recommendation — 10 August 2001 | |
CellML is intended to be used to represent many different types of models. Therefore, its basic structure is general. Models are primarily specified by explicitly defining mathematics using MathML. It is possible to specify a model purely in terms of mathematics, without using any of the elements defined in this section of the specification. However, in some types of models, information is lost when reducing the model to pure mathematics. For instance, in biochemical pathway models it will not always be straightforward, or even possible, to unambiguously determine from the mathematical rate laws which variables represent inhibitors or activators in the reactions. Therefore, some additional elements are needed in CellML to fully capture the information in biochemical pathway models.
Three fundamental representations of reaction/pathway models must be supported by CellML:
-
Mathematical Equations: These are any valid mathematical equations that describe the model. For example, they may be ordinary differential equations that define kinetic reaction rate laws and the rate of change of the concentration of species participating in the modelled reactions.
-
Chemical Expressions: These are the stoichiometric expressions (such as
A + B <-> 2C + D) used by chemists to represent reactions.
-
Pathway Diagrams: These are the stylised drawings commonly used by biochemists and cell biologists to represent interactions among participants in reactions. Some examples of pathway diagrams are shown in Section 7.3.
It is important that CellML be able to store the information needed to reproduce unambiguously any of these representations of a model. It is also important to minimise duplication of information within the model definition, because duplication can lead to inconsistencies. Therefore, CellML integrates the information needed to support the three types of model representation.
The integration process has resulted in the introduction of a CellML syntax that implies a mathematical relationship between variables in the current component. In this section of the specification, explicit mathematics refers to equations defined using MathML, and implicit mathematics refers to equations implied from the CellML syntax.
CellML supports both quantitative and qualitative pathway models. Many types of models are commonly referred to as "qualitative". Some of these are mathematically specified, while others are not. For the purposes of this specification, qualitative pathway models consist solely of information about how the different chemical species in the pathway relate, and contain no mathematics. However, the stoichiometry of the reactions may be known. In other words, there is no mathematical representation of the model, but there may still be a pathway diagram and chemical expressions that represent the model. Because a qualitative model has no mathematics, CellML processing software is not required to be able to run a simulation using a qualitative model. However, some software may support simple simulations using such models.
Any model in which the change of concentration of a chemical species participating in a reaction is implicitly or explicitly defined is a quantitative pathway model. All others are qualitative pathway models.
The <reaction> element is used to store information associated with a single reaction. It may only appear inside a <component> element. Examples demonstrating the use of the <reaction> element are presented in Section 7.3. It is possible for a single <component> element to contain more than one <reaction> element. However, this makes it difficult to re-use the individual reactions, and is therefore not the recommended best practice. The <reaction> element may define a reversible attribute, the value of which indicates whether or not the reaction is reversible. The default value of the reversible attribute is "yes".
The reaction element contains multiple <variable_ref> elements, each of which references a variable that participates in the reaction. The recommended best practice is to create a <variable_ref> element for each variable representing the concentration of a chemical species that participates in a reaction, as well as one for the variable representing the rate of the reaction. The required variable attribute is the only attribute on the <variable_ref> element. Its value is the name of the referenced variable. This variable must be declared in the current <component> element.
Each <variable_ref> element contains one or more <role> elements. A <role> element must not contain any elements in the CellML namespace, but may have up to four attributes. The required role attribute specifies the way in which the variable participates in the reaction. The role attribute must have a value of "reactant", "product", "catalyst", "activator", "inhibitor", "modifier", or "rate". The meaning associated with each value is defined in Section 7.4. The optional direction attribute may be used on <role> elements in reversible reactions. If defined, it must have a value of "forward", "reverse", or "both". Its value indicates the direction of the reaction for which the role is relevant. It has a default value of "forward". The optional delta_variable attribute indicates which variable is used to store the change in concentration of the species represented by the variable referenced by the current <variable_ref> element. The optional stoichiometry attribute stores the stoichiometry of the current variable relative to the other reaction participants. Section 7.4 contains detailed rules for the use of these attributes.
The <role> elements may also contain <math> elements in the MathML namespace, which define equations using MathML. Although it is not required, it is recommended best practice to store all of the equations that relate to a reaction inside the appropriate <role> elements in the <reaction> element. This makes the <reaction> element more re-usable. In addition, defining mathematics inside a <role> element has the effect of associating the equations with the variable referenced by the containing <variable_ref> element, in the role defined by the <role> element. This enables CellML processing software to present the equations in a more meaningful context. For instance, it may group all of the relationships between the rate variable and the delta variables for all of the reactants and products, or it may display these equations in a different color.
There are three uses for equations inside <role> elements:
-
If the
role attribute value is "rate", any enclosed equations calculate the kinetic rate law (i.e., calculate the value of the referenced variable) and the value of intermediate variables used in the rate law equation.
-
If the
role attribute value is "reactant" or "product", the equations calculate the relationship between the general reaction rate and the rate of change of the species represented by the referenced variable (i.e., calculate the value of the variable named in the delta_variable attribute), and calculate any intermediate variables used in this relationship.
-
In all other cases, the equations relate an intermediate variable used in the rate calculation to the variable referenced by the containing
<variable_ref> element. For instance, it would be appropriate to calculate an effective concentration of a catalyst inside the <role> element contained by the <variable_ref> element that references the variable representing the actual concentration of the catalyst.
CellML processing software is not required to be able to deduce the stoichiometry of a reaction from explicit mathematics. Therefore, it is strongly recommended that the stoichiometry and delta_variable attributes be used instead of explicit mathematics if the concentration change is simply the reaction rate multiplied by the stoichiometry. (The rules for deriving this mathematical relationship from the stoichiometry attribute are defined in Section 7.5.5.)
This section contains two examples demonstrating the recommended use of the <reaction>, <variable_ref> and <role> elements to define two basic reactions. The mathematics defining the reaction rate have been omitted in these examples. See the signal transduction model examples section of the CellML website for further examples.
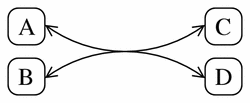
Figure 11 shows a pathway diagram representation of the following reversible reaction:
Figure 12 demonstrates the use of CellML to define this reaction. There are five <variable_ref> elements in the <reaction> element: one for each variable representing the concentration of a chemical species participating in the reaction, and one for the variable representing the general reaction rate. Note that the stoichiometry attribute has a value of "2" for the variable representing the chemical species C, since this species appears with a stoichiometry of 2 in the chemical expression. The reversible attribute on the <reaction> element and the direction attributes on the <variable_ref> elements have their default values ("yes" and "forward", respectively) and therefore could have been omitted, but they are included for clarity.
Figure 11
A typical pathway diagram representation of the simple reversible reaction A + B <-> 2C + D.
<reaction reversible="yes">
<variable_ref variable="A">
<role
role="reactant" direction="forward"
delta_variable="delta_A" stoichiometry="1" />
</variable_ref>
<variable_ref variable="B">
<role
role="reactant" direction="forward"
delta_variable="delta_B" stoichiometry="1" />
</variable_ref>
<variable_ref variable="C">
<role
role="product" direction="forward"
delta_variable="delta_C" stoichiometry="2" />
</variable_ref>
<variable_ref variable="D">
<role
role="product" direction="forward"
delta_variable="delta_D" stoichiometry="1" />
</variable_ref>
<variable_ref variable="r">
<role role="rate">
<math xmlns="http://www.w3.org/1998/Math/MathML">
... <!-- reaction rate math -->
</math>
</role>
</variable_ref>
</reaction>
Figure 12
The CellML definition of the simple reversible reaction A + B <-> 2C + D. See text for more details.
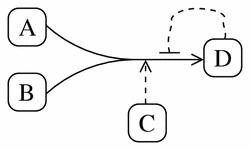
Figure 13 shows the pathway diagram for the following irreversible, catalyzed reaction, which exhibits product-inhibition:
A + B -> D (catalyzed by C, inhibited by D)
The CellML definition of this reaction is shown in Figure 14.
Figure 13
A typical pathway diagram representation of the irreversible reaction A + B -> D (catalyzed by C, inhibited by D).
<reaction reversible="no">
<variable_ref variable="A">
<role role="reactant" delta_variable="delta_A" stoichiometry="1" />
</variable_ref>
<variable_ref variable="B">
<role role="reactant" delta_variable="delta_B" stoichiometry="1" />
</variable_ref>
<variable_ref variable="C">
<role role="catalyst" />
</variable_ref>
<variable_ref variable="D">
<role role="product" delta_variable="delta_D" stoichiometry="1" />
<role role="inhibitor" stoichiometry="1" />
</variable_ref>
<variable_ref variable="r">
<role role="rate">
<math xmlns="http://www.w3.org/1998/Math/MathML">
... <!-- reaction rate math -->
</math>
</role>
</variable_ref>
</reaction>
Figure 14
The CellML definition of the irreversible reaction A + B -> D (catalyzed by C, inhibited by D). See text for more details.
The <variable_ref> element that references the variable representing the concentration of species D now contains two <role> elements, one with information about D as a product and the other with information about D as an inhibitor. In this example, D has the same stoichiometry in both roles, but this would not necessarily need to be the case.
- Allowed use of the
<reaction> element
-
A <component> element may contain any number of <reaction> elements.
[ The use of multiple <reaction> elements within a single <component> element is discouraged. ]
-
A <reaction> element must contain only the following elements,
which may appear in any order:
-
<variable_ref> elements in the CellML namespace,
<RDF> elements in the RDF namespace.
[ The recommended best practice is to define one <variable_ref> element for each variable representing a chemical species that participates in the reaction, and one <variable_ref> element for the variable representing the rate of the reaction. ]
-
Each <reaction> element must contain at least one <variable_ref> element.
-
The <reaction> element may define a reversible attribute.
- Allowed values of the
reversible attribute
-
If present, the reversible attribute must have a value of "yes" or "no".
-
If not present, the value of the reversible attribute defaults to "yes".
[ It is recommended to always explicitly define the value of this attribute. ]
- Proper use of the
<reaction> element in encapsulating components
[ It is often convenient to include a <reaction> element in a component that is encapsulating several intermediate reactions (see Section 6 for more information about encapsulation). The encapsulating component represents an overall, or total, reaction, which can be represented by a <reaction> element. This total reaction is effectively qualitative, because the mathematics representing the progression of the total reaction are defined in the components representing the intermediate reactions. ] -
A <reaction> element in an encapsulating component must not contain delta_variable attributes on the <role> elements or explicit mathematics defining the overall reaction rate or the changes in concentration of the species that participate in the total reaction.
[ A CellML document should not define an inconsistent set of equations. This rule prevents authors inadvertantly introducing explicit or implicit mathematics in an encapsulating component that duplicates or contradicts mathematics (either explicit or implicit) defined in the encapsulated components. ]
- Allowed use of the
<variable_ref> element
-
A <variable_ref> element must contain only the following elements,
which may appear in any order:
<role> elements in the CellML namespace,
<RDF> elements in the RDF namespace.
-
Each <variable_ref> element must contain at least one <role> element.
[ The recommended best practice is to define one <role> element for each role assumed by the chemical species represented by the referenced variable. ]
-
Each <variable_ref> element must define a variable attribute.
- Allowed values of the
variable attribute
-
The value of the variable attribute on a <variable_ref> element within a <reaction> element must equal the value of the name attribute on a <variable> element defined inside the current <component> element.
-
The value of the variable attribute must be unique across all <variable_ref> elements contained within the parent <reaction> element.
[ A variable must only be referenced once in a single reaction. ]
- Allowed use of the
<role> element
-
A <role> element must contain only the following elements,
which may appear in any order:
-
<math> elements in the MathML namespace,
<RDF> elements in the RDF namespace.
[ Some rules for the use of mathematics in <role> elements are provided below, and rules for the <math> element and its children are given in Section 4. ]
-
Each <role> element must define a role attribute. It may also define delta_variable, direction, and stoichiometry attributes.
- Allowed values of the
role attribute
- Proper use of the
role attribute
-
A <reaction> element must contain no more than one <variable_ref> element with a <role> element with a role attribute with a value of "rate".
[ There may only be one rate variable per reaction. ]
-
A <variable_ref> element that contains a <role> element with a role attribute value of "rate" must not contain other <role> elements.
[ The variable assigned the "rate" role may not be assigned any other roles. ]
-
A <role> element with a role attribute value of "rate" must not define delta_variable or stoichiometry attributes.
[ The delta_variable and stoichiometry attributes have no meaning for a rate variable. ]
- Allowed values of the
direction attribute
-
If present, the direction attribute must take one of the following three values:
-
"forward": the value of the role attribute is the role of the referenced variable in the reaction when running in the "favoured" direction. The favoured direction is the one in which the the reactants are being consumed (i.e., the time-derivatives of their concentrations are negative), as defined by the kinetic rate law.
-
"reverse": the value of the role attribute is the role of the referenced variable in the reaction when running opposite to the "favoured" direction. In this direction, the reactants (as defined by the kinetic rate law) are being produced.
-
"both": the value of the role attribute is the role of the referenced variable in both directions of the reaction.
-
If not present, the value of the direction attribute defaults to "forward".
- Proper use of the
direction attribute
-
A direction attribute on a <role> element that is inside a <reaction> element with a reversible attribute value of "no" must have a value of "forward".
[ Only reversible reactions may occur in two directions. ]
-
A direction attribute on a <role> element for which the role attribute has a value of "rate", "reactant" or "product" must have a value of "forward".
[ Variables representing the reaction rate, a reactant or a product should always be labelled as such in the forward direction. To do otherwise would cause the implicit mathematics defined by the delta_variable and stoichiometry attributes on the reactant and product variables to be erroneous. ]
-
Each <role> element contained in a given <variable_ref> element must have a unique combination of values for the role and direction attributes.
[ Defining two <role> elements with the same role and direction attribute values would allow the definition of inconsistent stoichiometries or multiple delta variables for a single variable. Both of these situations would imply inconsistent mathematics. ]
- Allowed values of the
stoichiometry attribute
-
If present, the value of the stoichiometry attribute must be a real number.
[ In most cases, the value will be an integer. However, a valid CellML model may use fractional stoichiometries. ]
- Allowed values of the
delta_variable attribute
-
If present, the value of the delta_variable attribute must equal the name attribute on a <variable> element defined inside the current <component> element.
-
If present, the value of the delta_variable attribute must be unique across all <role> elements contained within the parent <component> element.
[ One variable cannot represent the rate of change in concentration of more than one species. The value of the delta_variable attribute must be unique across the entire <component> element because it is legal (but not recommended) to include more than one <reaction> element in a single component. ]
- Proper use of the
delta_variable attribute
-
A delta_variable attribute must only appear on <role> elements in which the role attribute has a value of "reactant" or "product".
[ It is only in these roles that a chemical species may undergo a change in concentration. ]
-
A <role> element on which a delta_variable attribute is declared must also either declare a stoichiometry attribute or contain at least one <math> element in the MathML namespace.
[ The combination of the delta_variable attribute and the stoichiometry attribute implies a mathematical relationship between the variable referenced in the delta_variable attribute and the variable assigned the role of "rate", as defined in Section 7.5.5. If the stoichiometry attribute is absent, the relationship between the variable assigned the role of "rate" and the variable named in the delta_variable attribute must be defined using MathML. ]
-
A <role> element on which the stoichiometry and delta_variable attributes are both defined must not contain <math> elements in the MathML namespace.
[ The equations in a <math> element inside a <role> element for which the role attribute is "reactant" or "product" must relate the variable named in the delta_variable attribute to the variable assigned the role of "rate". Such equations would contradict the relationship implied by the delta_variable and stoichiometry attributes, as defined in Section 7.5.5. ]
-
If the delta_variable and stoichiometry attributes are both declared on any single reaction participant, a <variable_ref> element must be provided for the variable that represents the reaction rate. This <variable_ref> must contain exactly one <role> element, with a role attribute equal to "rate".
[ The reverse is not true: a variable may be assigned a role of "rate" even if the "reactant" and "product" variables do not define delta_variable attributes. In this case, the modeller may choose to provide explicit mathematics relating the "rate" variable to the change in concentration of the various chemical species. ]
- Proper use of a
<math> element inside a <role> element
-
A <math> element in the MathML namespace inside a <role> element must define equations that are relevant to the variable referenced by the containing <variable_ref> element, acting in the role defined by the role attribute on the <role> element.
[ The meaning of "relevant" in this context is discussed in Section 7.5.6. ]
If the reversible attribute on a <reaction> element has a value of "yes", it is assumed that all reactants in the forward direction are products in the reverse direction and vice versa. Similarly, all products in the forward direction are assumed to be reactants in the reverse direction and vice versa.
CellML processing software must not make any assumptions if a stoichiometry attribute is not defined on a <role> element. The absence of a stoichiometry value specifically does not imply a stoichiometry of "1". Instead, it would usually mean that the stoichiometry of the reaction is unknown.
The value of the stoichiometry attribute on a <role> element is defined to be the stoichiometry of the chemical species whose concentration is represented by the variable referenced by the containing <variable_ref> element. This stoichiometry can be used to produce the chemical expression representation of the model.
CellML processing software must not make any assumptions if a delta_variable attribute is not defined on a <role> element.
The use of the delta_variable and stoichiometry attributes on a <role> element implies the following mathematical relationship between the declared delta variable and the rate variable (where the variable representing the reaction rate will have a negative value when the reaction is proceeding in the forward direction):
-
For reactants:
delta_variable = (stoichiometry)(rate)
-
For products:
delta_variable = -(stoichiometry)(rate)
The two reactions shown in Figure 15 are mathematically equivalent. The representation in the first reaction in Figure 15 is the recommended best practice, because processing applications are not required to be able to extract the stoichiometry from an explicit MathML definition such as the one shown in the second reaction.
Explicit mathematics should only be used in cases where the implicit formulation would be inappropriate. Some examples of such cases are:
-
If the stoichiometry of a reaction is unknown, but the modeller still wishes to relate the rate of change of a particular chemical species to the general reaction rate. Defining the
stoichiometry attribute implies that the stoichiometry is known to equal the value of that attribute.
-
If the modeller wishes to experiment with the stoichiometry of a species in different simulations using the model. (In this case, it might be easier if the stoichiometry is defined as a variable.)
-
If the math implied from the recommended formulation would be incorrect, i.e., in the rare cases when a more complex function is needed to relate the change in concentration of a species to the reaction rate.
In all of these cases, it is recommended best practice to put the mathematical expression used to define the change in concentration of a species inside the <role> element contained in the <variable_ref> element referring to the variable representing the concentration of that species.
<!--
The recommended best practice for calculating the value of delta_A, which
is an implied function of stoichiometry and reaction rate.
-->
<reaction reversible="yes">
<variable_ref variable="A">
<role
role="reactant" direction="forward"
delta_variable="delta_A" stoichiometry="2" />
</variable_ref>
<variable_ref variable="r">
<role role="rate">
<math xmlns="http://www.w3.org/1998/Math/MathML">
... <!-- reaction rate math -->
</math>
</role>
</variable_ref>
</reaction>
<!--
In this reaction, the value of delta_A is calculated explicitly using MathML.
This is not the recommended best practice.
-->
<reaction reversible="yes">
<variable_ref variable="A">
<role
role="reactant" direction="forward"
delta_variable="delta_A">
<math xmlns="http://www.w3.org/1998/Math/MathML">
<apply><eq />
<ci> delta_A </ci>
<apply><times />
<cn cellml:units="dimensionless"> 2.0 </cn>
<ci> r </ci>
</apply>
</apply>
</math>
</role>
</variable_ref>
<variable_ref variable="r">
<role role="rate">
<math xmlns="http://www.w3.org/1998/Math/MathML">
... <!-- reaction rate math -->
</math>
</role>
</variable_ref>
</reaction>
Figure 15
The top <reaction> element shows the recommended best practice for defining the change in concentration delta_A of a chemical species A with respect to the reaction rate r. The second <reaction> element shows an equivalent representation using an explicit MathML definition. Use of this formulation is not recommended. The MathML blocks defining the rate laws are omitted.
It is an error to explicitly declare mathematics that conflicts with or duplicates implied mathematics. Therefore, a modeller must not declare a stoichiometry attribute and delta_variable attribute in addition to explicit math relating the change in concentration of the referenced species to the reaction rate.
Equations defined in <math> elements in the MathML namespace inside a <role> element must be relevant to the the variable referenced by the parent <variable_ref> element, acting in the role defined by the value of the role attribute. This means that:
-
If the
role attribute value is "rate", the equations must calculate the kinetic rate law (i.e., calculate the value of the referenced variable). Intermediate calculations related to the calculation of the rate are also allowed. Conventionally, the variable representing the reaction rate will have a negative value when the reaction is proceeding in the forward direction.
-
If the
role attribute value is "reactant" or "product", the equations must calculate the relationship between the general reaction rate and the rate of change of the species represented by the referenced variable (i.e., calculate the value of variable named in the delta_variable attribute). Intermediate calculations related to the calculation of the delta variable are also allowed.
-
In all other cases, the equations must relate an intermediate variable used in the rate calculation to the variable referenced by the containing
<variable_ref> element. For example, it would be appropriate to calculate an effective concentration of an inhibitor or catalyst in the <role> element contained in the <variable_ref> element that references the variable representing the actual concentration of that species.
Duplication of information is avoided as much as possible. However, because modellers must be free to define arbitrary rate laws, it was not possible to eliminate all information duplication. For instance, CellML processing software is not expected to be able to deduce all information about a reaction from kinetic laws of arbitrary form, even though most information is in fact represented in these laws. Therefore, there is a possibility that the information in the mathematics and the information in the <reaction> element may be inconsistent.
It is anticipated that most modellers will define CellML models using some sort of processing software, which can reasonably be expected to write consistent mathematics. However, since CellML is a text-based format, modellers may also create or edit models by hand, and in doing so risk creating inconsistent models.
The following rules govern the required behaviour of CellML conformant processing software in the event that information in the explicitly and implicitly defined mathematics do not agree:
-
CellML processing software may check for inconsistencies between mathematics explicitly defined using MathML and mathematics implicitly defined using the attributes on the
<role> element. If software does check, it is recommended that it notify the user if inconsistencies are detected.
-
If inconsistencies are found, CellML processing software must use mathematics explicitly defined using MathML when running a simulation with the model.
-
CellML processing software may treat inconsistencies as it chooses when representing the model. For instance, software may ignore inconsistencies when rendering pathway diagrams or chemical expressions.
|  |  |  |  |  |