CellML Specification Final Draft — 18 May 2001

Get the PDF!

A  Using The CellML 1.0 DTD

A.1  Introduction

This section contains some recommendations on the use and referencing of the CellML 1.0 DTD, the full text of which is given in Appendix A.6. The document rules and processor behaviour described in this section are not required in valid CellML documents and from CellML compliant processing software, respectively.

A.2  The CellML DOCTYPE declaration

CellML documents that reference the CellML 1.0 DTD should contain a DOCTYPE declaration of the following form:

<!DOCTYPE model SYSTEM "http://www.cellml.org/cellml/cellml_1_0.dtd">

"model" may be changed to match the root element of the CellML document.

CellML document authors may change the value of the system identifier to point to a copy of the DTD cached on a local filesystem if this is available. This specification does not define a public identifier for CellML 1.0. For interoperability, CellML document authors should not define one unless specifically needed for a parser that makes use of SGML catalog files.

A.3  CellML without a DTD

CellML documents are not required to contain a DOCTYPE declaration. In the absence of a DTD, CellML processing software needs to take into account the following important points:

• All cmeta:id attributes are of type ID.
• All id attributes on MathML elements are of type ID.

The CellML DTD does not define the default values for CellML attributes that are defined in the specification. With or without a DTD, CellML processing software is responsible for setting these values, if not specified.

A.4  Use of MathML within CellML

The CellML 1.0 DTD provides facilities for including the MathML 2.0 DTD using a relative path. The reference to the MathML DTD is inside a conditional section of the CellML DTD, and by default the reference is ignored. CellML document authors with a copy of both the CellML and MathML DTDs on the local filesystem may validate against both by causing the contents of the conditional section to be included using a DOCTYPE declaration of the following form:

<!DOCTYPE model SYSTEM "/my/local/copy/of/the/cellml_1_0.dtd" [
  <!ENTITY % mathml_dtd_path "'relative/path/to/mathml2.dtd'">
  <!ENTITY % use_mathml_dtd "INCLUDE">
]>

The MathML 2.0 DTD is not on the CellML website, so DOCTYPE declarations of this form will fail when referencing the DTD on the CellML website. The MathML 2.0 DTDs are available as a ZIP archive, a link to which is given in Appendix A.6 of the MathML 2.0 Recommendation.

The CellML specification requires a cellml:units attribute to be defined on all <mathml:cn> elements (where the cellml and mathml prefixes are mapped to the URIs for the CellML and MathML namespaces, respectively). For this reason, the conditional section of the CellML DTD in which the MathML DTD is referenced also redeclares the list of attributes on the <mathml:cn> element to include the cellml:units attribute. This will prevent XML parsers from finding errors when validating valid CellML documents against the MathML DTD.

A.5  Treatment of namespaces

In Section 2.2.2, it was suggested that the root element of a CellML document set the default namespace and map the cellml prefix to the CellML namespace URI. Use of unprefixed element names (i.e., default namespaces) is encouraged to ensure DTD-based validation will work correctly. The CellML 1.0 DTD defines three optional attributes on every CellML element that can be used to set namespaces where necessary. These are xmlns, xmlns:cellml and xmlns:cmeta.

A.6  The CellML 1.0 DTD

The CellML 1.0 DTD is available at the following URI:

The CellML 1.0 DTD does not attempt to declare or reference declarations for the metadata framework elements in the RDF namespace. It also doesn't declare the default values of any of the attributes on the CellML elements.

For convenient reference, the text of the DTD is given below.

<!--
FILE : cellml_1_0.dtd

CREATED : 22 January 2001

LAST MODIFIED : 17 May 2001

AUTHOR : Warren Hedley (w.hedley@auckland.ac.nz)
         The Bioengineering Research Group
         The University of Auckland

DESCRIPTION : This document contains a DTD corresponding to the syntax rules
  defined in the 18 May 2001 Final Draft Specification for CellML 1.0. This
  specification is available at
    http://www.cellml.org/public/specification/20010518/index.html

PUBLIC IDENTIFIER : To be announced.

SYSTEM IDENTIFIER : http://www.cellml.org/cellml/cellml_1_0.dtd

COPYRIGHT : To be announced.
-->

<!ENTITY % use_mathml_dtd "IGNORE">
<![%use_mathml_dtd;[
  <!ENTITY % mathml-charent.module "IGNORE">
  <!ENTITY % mathml_dtd_path "'MathML-20010221/mathml2.dtd'">
  <!ENTITY % mathml_dtd PUBLIC "-//W3C//DTD MathML 2.0//EN"
     %mathml_dtd_path;>

  %mathml_dtd;

  <!ATTLIST %cn.qname;    
    %MATHML.Common.attrib;
    %att-type;
    %att-base;
    %att-definition;
    %att-encoding;
    cellml:units      CDATA           #REQUIRED
  >
]]>

<!ENTITY % cellml_common_attributes "
  xmlns               CDATA           #IMPLIED
  xmlns:cellml        CDATA           #IMPLIED
  xmlns:cmeta         CDATA           #IMPLIED
  cmeta:id            ID              #IMPLIED
">

<!ELEMENT model (units | component | group | connection)*>
<!ATTLIST model
  %cellml_common_attributes;
  name                CDATA           #REQUIRED
>

<!ELEMENT component (units | variable | reaction | math)*>
<!ATTLIST component
  %cellml_common_attributes;
  name                CDATA           #REQUIRED
>

<!ELEMENT variable EMPTY>
<!ATTLIST variable
  %cellml_common_attributes;
  name                CDATA           #REQUIRED
  public_interface    (in|out|none)   #IMPLIED
  private_interface   (in|out|none)   #IMPLIED
  units               CDATA           #REQUIRED
  initial_value       CDATA           #IMPLIED
>

<!ELEMENT connection (map_components, map_variables+)>
<!ATTLIST connection
  %cellml_common_attributes;
>

<!ELEMENT map_components EMPTY>
<!ATTLIST map_components
  %cellml_common_attributes;
  component_1         CDATA           #REQUIRED
  component_2         CDATA           #REQUIRED
>

<!ELEMENT map_variables EMPTY>
<!ATTLIST map_variables
  %cellml_common_attributes;
  variable_1          CDATA           #REQUIRED
  variable_2          CDATA           #REQUIRED
>

<!ELEMENT units (unit*)>
<!ATTLIST units
  %cellml_common_attributes;
  name                CDATA           #REQUIRED
>

<!ELEMENT unit EMPTY>
<!ATTLIST unit
  %cellml_common_attributes;
  multiplier          CDATA           #IMPLIED
  prefix              CDATA           #IMPLIED
  units               CDATA           #REQUIRED
  exponent            CDATA           #IMPLIED
  offset              CDATA           #IMPLIED
>

<!ELEMENT group (relationship_ref+, component_ref+)>
<!ATTLIST group
  %cellml_common_attributes;
>

<!ELEMENT relationship_ref EMPTY>
<!ATTLIST relationship_ref
  %cellml_common_attributes;
  relationship        CDATA           #REQUIRED
>

<!ELEMENT component_ref (component_ref*)>
<!ATTLIST component_ref
  %cellml_common_attributes;
  component           CDATA           #REQUIRED
>

<!ELEMENT reaction (variable_ref+)>
<!ATTLIST reaction
  %cellml_common_attributes;
  reversible          (yes|no)        #IMPLIED
>   

<!ELEMENT variable_ref (role+, math*)>
<!ATTLIST variable_ref
  %cellml_common_attributes;
  variable            CDATA           #REQUIRED
>

<!ELEMENT role (math?)>
<!ATTLIST role
  %cellml_common_attributes;
  role (reactant|product|activator|catalyst|inhibitor|modifier|rate) #REQUIRED
  direction (forward|backward|both)   #IMPLIED
  delta_variable      CDATA           #IMPLIED
  stoichiometry       CDATA           #IMPLIED
>

B  Scripting functionality in CellML

B.1  Introduction

MathML can be extended by defining new operators, the behaviour of which is not defined in MathML. These operators could be used to call functions implemented in software (i.e., implicitly) or defined using a scripting language (i.e., explicitly). CellML 1.0 does not require processing software to implement support for scripting functionality. This section contains some recommendations on best practices for adding scripting functionality to CellML.

For the purposes of this discussion, it is assumed that scripting functionality will be implemented via function calls. Software that extends the functionality of MathML in other ways should extrapolate these recommendations as appropriate.

B.2  Availability of scripts

Functions referenced in a CellML document that are defined using non-MathML syntax should be identified by, and accessible via, a URI. A function could, for instance, be accessible via HTTP from a database using a CGI script that takes an SQL expression as an argument.

B.3  Embedding scripts in CellML

Functions should be defined within elements in an application-specific extension namespace, if the functions are embedded within CellML documents. If the embedded script is only referenced by a single component, the script should be defined within the corresponding <cellml:component> element. If the embedded script is referenced by more than one component, the script should be defined within the <cellml:model> element.

B.4  Preferred scripting language

Implementors considering adding scripting functionality to CellML processing software are encouraged to use ECMAScript. It is anticipated that, when scripting functionality is officially endorsed by a future version of CellML, ECMAScript will be the scripting language that processing software is required to implement. ECMAScript is the recommended language because it is simple, standardised, and open source interpreting libraries are freely available.

ECMA is an international industry association that develops standards in information and communication for the European union. ECMA took the scripting language that Netscape developed for adding interactive content to its web browser and developed the formal language specification ECMA-262 (ECMAScript Language Specification).

B.5  Referencing scripts from MathML

The MathML 2.0 Recommendation defines a <mathml:csymbol> element for referencing mathematical symbols and constructs that are not defined by MathML. This element should be used for referencing functions defined using non-MathML syntax from within blocks of MathML. Processing software should take into account the following recommendations regarding the use of the <mathml:csymbol> element for this purpose.

B.5.1  The <mathml:csymbol> element

1. Recommended use of the <mathml:csymbol> element

   • The <mathml:csymbol> element should only appear as the first child element within a <mathml:apply> element.

     [ A <mathml:csymbol> element should only be used as an operator, which is "applied" to some arguments. ]

   • After leading and trailing whitespace is removed, the content of a <mathml:csymbol> element must be a valid CellML identifier as discussed in Section 2.2.1. This identifier must accurately represent the external function referenced.

     [ The content of a <mathml:csymbol> element should preferably be a human-readable identifier for the external function. If the function is defined using a common scripting or programming language, then this identifier should be the name of the function. ]

   • Each <mathml:csymbol> element should define a definitionURL and an encoding attribute.

2. Recommended use of the mathml:definitionURL attribute

   • The value of the definitionURL attribute should be a valid URI that identifies a single resource containing the definition of the external function.

3. Recommended use of the mathml:encoding attribute

   • The value of the encoding attribute should indicate to processing software the format of the externally defined function.

     [ In the version of CellML that describes how external functions are to be defined within the CellML framework, the encoding attribute will be moved into the CellML namespace and will be required to take a value from a controlled vocabulary. ]

B.6  Effects of scripts

Scripts should be side-effect free. That is, scripts should not alter the values of of their arguments.

C  Advanced Units Functionality

C.1  Introduction

CellML 1.0 lays the foundations of a flexible and robust system for the association of units with variables and constants in cellular models. However, it does not require software to make use of the units information contained in CellML documents. This section presents algorithms and examples demonstrating some of the advanced features related to units that CellML processing software might choose to offer modellers. For interoperability, CellML processing software that includes these features should achieve the same results as the algorithms described here, although the exact implementation may differ.

C.2  Terminology

C.2.1  Equivalence of units references

Two units references are considered equivalent if they satisfy one of the following criteria:

• They reference the same units definition from the standard dictionary.
• They reference the same units definition in the current <component> element.
• They reference the same units definition in the current <model> element, where that units definition is not superceded by a units definition with the same name in the current <component> element.

C.2.2  Dimensional equivalence of units definitions

Two units definitions have dimensional equivalence if, when each is recursively expanded and simplified until left with nothing but products of SI and user-defined base units:

• the expanded form of each units definition consists of the same set of base units, and
• the exponent on each base unit is identical in each expanded units definition.

Algorithms for the expansion and simplification of units definitions are given in Appendix C.3.4 and Appendix C.3.1, respectively.

C.3  Algorithms

C.3.1  Simplification of units definitions

It is frequently convenient to be able to simplify a units definition, where this units definition is the result of the application of some mathematical operator to terms which have units associated with them. These operators include the <times>, <divide> and <diff> operators.

The simplification of a units definition is an iterative process in which the number of other units definitions referenced is systematically reduced. References to units definitions may be removed in the following cases:

• If two units references are equivalent (as defined in Appendix C.2.1) and have exponents with equal and opposite value, then they may be replaced by a reference to dimensionless.
• If two units references are equivalent (as defined in Appendix C.2.1) then they may be replaced with a single units reference to the same units, where the exponent associated with that units reference is the sum of the exponents on the original two units references.
• If a units definition references dimensionless one or more times in addition to some other units, any references to dimensionless may be removed.
• If a units definition references dimensionless one or more times and references no other units, the definition may be replaced with dimensionless.

The above rules only allow the removal of units references that are equivalent as defined in Appendix C.2.1. This scheme would not allow references to identical units definitions in two different components to be cancelled and removed, because the references would not satisfy the equivalence criteria.

C.3.2  Units-based restrictions on the use of MathML operators

This section describes restrictions on the units associated with a collection of terms to which each MathML operator in the CellML set (defined in Section 4.2.3) can be applied. For instance, the <mathml:plus> operator can only be applied to terms that have dimensionally equivalent units. The restrictions invalidate the application of certain MathML operators to certain collections of terms based on their units, and are used in equation dimension checking, as described in Appendix C.3.6.

The restrictions are given in Table 5. Note that the <mathml:root>, <mathml:diff> and <mathml:log> elements all take qualifiers, in addition to operands.

Table 5 The restrictions on the units associated with operands and qualifiers for each MathML operator. All elements in this table are in the MathML namespace.

C.3.3  Applying operators to units definitions

The section defines the units resulting from the application of MathML operators to a collection of terms, each with known units. This is needed for units definition conversion and equation dimension checking, as described in Appendix C.3.5 and Appendix C.3.6, respectively. The units on each of the terms in the collection must satisfy the restrictions defined in Appendix C.3.2 for the current operator.

The full set of units calculation rules are described in Table 6.

Table 6 The units of the result after applying each MathML operator to a collection of terms, where the units on those terms satisfy the restrictions in Appendix C.3.2. All elements in this table are in the MathML namespace.

C.3.4  Expansion of units definitions

This section presents the recommended algorithm for expanding a given units definition into an expression that relates the defined units to only SI and user-defined base units. This algorithm may be used in the conversion of units definitions and equation dimension checking, algorithms for which are defined in Appendix C.3.5 and Appendix C.3.6, respectively. Examples of the expansion of units definitions are given in Appendix C.4.2.

The specific steps in the algorithm depend on whether the units definition to be expanded is simple or complex, as defined in Section 5.2.2. Both derivations use recursive methods. At each step, any units that are not base units are replaced with expansions based on the appropriate definition.

Expansion of simple units definitions

The formula relating a variable x_U with units of U (where U are simple units), to a variable x₁ with units of u1 (the subunits referenced by the units attribute on the <unit> element inside the units definition for U), is given in Equation 9. This is based on the simple units definition formula given in Equation 3.

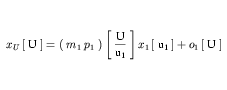(9)

m₁, p₁ and o₁ correspond to the multiplier, prefix and offset attributes on the <unit> element, respectively.

The formula relating a variable with units of u1 to its subunits u2, as referenced in the units definition for u1, is given in Equation 10.

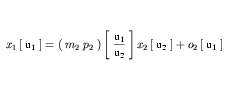(10)

Equation 10 can be substituted into Equation 9 to give Equation 11.

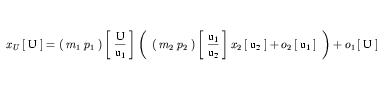(11)

The expression defining each new set of units in terms of its subunits can be substituted into the current expression recursively until an expression is reached that relates x_U to x_n with units un, which are SI or user-defined base units. At this point expansion stops, and the resulting expression can be simplified. This simplification combines multiplier, prefix and offset terms and combines their units based on the rules defined in Appendix C.3.3. The result is an expression of the form given in Equation 12.

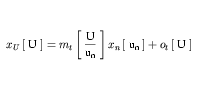(12)

The values of m_t and o_t are given by Equation 13 and Equation 14, respectively.

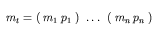(13)

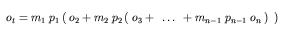(14)

Expansion of complex units definitions

The formula relating a variable x_U with complex units U to a variable x_A with units that are the product of the subunits referenced in the units definition for U is given in Equation 15. This is based on the complex units definition formula given in Equation 4.

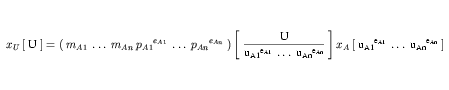(15)

The m_Ai, p_Ai, uAi and e_Ai refer to the values of the multiplier, prefix, units and exponent attributes on the i-th <unit> element inside the units definition for U, respectively. If, at the first step, the c-th set of units referenced is not SI or user-defined base units, the formula relating uAc to the c-th set of units referenced to its subunits is given in Equation 16.

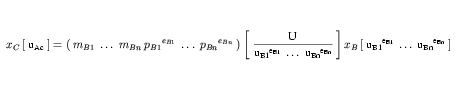(16)

Note that if uAc is a simple units definition, then the right hand side of Equation 16 will take the form of a simple units definition, but without the constant offset term.

An expansion for x_A that incorporates the expansion for uAc is obtained by multiplying both sides of Equation 16 by unitary coefficients with units of the product of all of the units referenced on the right hand side of Equation 15 with the exception of uAc. Expansion of units definitions involves constructing expansions for the variable on the right hand side. The expansion continues recursively as long as any of the units on the right hand side of Equation 15 are not SI or user-defined base units. The resulting expansion can be simplified by combining multiplier and prefix terms to give an expression with the form given in Equation 17.

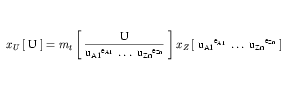(17)

uIi corresponds to the units referenced by the i-th units definition referenced in the I-th definition to be expanded, and m_t is given by Equation 18.

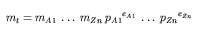(18)

m_Ii, p_Ii and e_Ii correspond to the values of the multiplier, prefix and exponent attributes on the i-th <unit> element in the I-th definition to be expanded.

C.3.5  Conversion between units definitions

This section presents an algorithm that specifies a possible method for converting a variable's value from one set of units to another. An example demonstrating the use of this algorithm is given in Appendix C.4.3.

If the two variable declarations that are to be mapped both reference equivalent units definitions as defined in Appendix C.2.1, then there is a one-to-one mapping between the the variable's value in both components.

If the two variable declarations that are to be mapped reference different units definitions, then software may choose to calculate a conversion formula as follows. Given a variable x with units Ux, the value of which is to be passed to a variable y with units Uy, the following steps should be followed:

1. The units definitions for Ux and Uy are fully expanded and simplified according to the algorithm presented in Appendix C.3.4. This yields expressions for x and y in terms of x_n and y_n, the units of which are products of only SI and user-defined base units. The expression for x will be of the form given in Equation 19 if Ux is a simple units definition, or of the form given in Equation 20 if Ux is a complex units definition.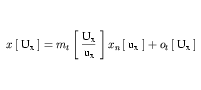

   (19)

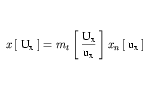
   (20)

   In Equation 19, ux corresponds to the base units referenced in the full expansion of Ux, whereas in Equation 20, ux corresponds to the product of all of the base units in the full expansion raised to the appropriate exponents.

2. It should be considered an error if the units for x_n (ux) and y_n (uy) do not have equivalent dimensions as defined in Appendix C.2.2.

3. The expansion of x is inverted to give an expression for x_n. The inverted forms of Equation 19 and Equation 20 are given in Equation 21 and Equation 22, respectively.

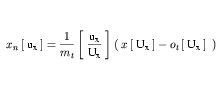
   (21)

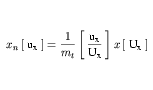
   (22)

   The appropriate expression for x_n can then be substituted for y_n in the expansion of y. This yields an equation for y in terms of x, which can be used to convert variable values.

C.3.6  Equation dimension checking

This section presents an algorithm that can be used to verify that an equation is consistent with respect to the dimensions of the units definitions referenced by all numbers and variables. An example that demonstrates the process of equation dimension checking for an equation defined in MathML and CellML is given in Appendix C.4.4.

This algorithm relies on the restrictions and behaviour of the different operators with respect to units defined in Appendix C.3.2 and Appendix C.3.3. Future versions of the specification may extend this algorithm to handle other operators. The steps in the algorithm are:

1. The equation is split into a tree of terms, in which each parent term is obtained by the application of a single operator to its children. The root of the tree is the entire equation, which is created by applying a relational operator (typically the equals operator) to its child terms. All other terms in the tree are created by applying arithmetic operators to child terms.

2. The units definitions for the terms at the leaves of the tree (which will be variables, numbers, or MathML constants elements) are expanded into functions of the SI and user-defined base units, using the algorithm presented in Appendix C.3.4.

3. Starting at the leaves of the tree, sets of child terms are recursively removed from the tree and units assigned to the parent terms. The removal of each set of terms follows the following steps:

   1. The child terms are compared against the restrictions described in Appendix C.3.2 for the current operator. It should be considered an error if they do not satisfy these restrictions, in which case the equation has inconsistent dimensions.

   2. Units are assigned to the parent term as defined in Appendix C.3.3 for the current operator.

4. The equation has self-consistent dimensions if no inconsistencies were found during the recursive removal of child terms during the traversal from leaves to root.

C.4  Examples

C.4.1  User-defined units and new base units

In Figure 17, the example units definitions given in Section 5.3 are reproduced. These examples are used in the subsequent advanced examples.

<!-- User-defined Base Units -->
<units name="pH" base_units="yes" />

<!-- Simple Units Definitions -->
<units name="inch">
  <unit multiplier="2.54" prefix="centi" units="metre" />
</units>

<units name="fahrenheit">
  <unit multiplier="1.8" units="celsius" offset="32.0" />
</units>

<!-- Complex Units Definitions -->
<units name="celsius_per_centimetre">
  <unit units="celsius" />
  <unit prefix="centi" units="metre" exponent="-1" />
</units>

<units name="fahrenheit_per_inch">
  <unit units="fahrenheit" />
  <unit units="inch" exponent="-1" />
</units>

<units name="pH_per_celsius">
  <unit units="pH" />
  <unit units="celsius" exponent="-1" />
</units>

Figure 17 Some examples of the use of the <units> element demonstrating the definition of simple and complex units.

C.4.2  Expansion of user-defined units

In this section, the expansion of user-defined units according to the algorithm described in Appendix C.3.4 is demonstrated for each of the units definitions given in Figure 17.

The first <units> element in Figure 17 defines units named pH, and defines a base_units attribute with a value of "yes". This indicates that it should be treated by processing software as if it were an SI base unit, and that it cannot be expanded.

The definition of inch in Figure 17 is a simple units definition as it references only a single unit with an exponent of one. When the appropriate terms are substituted into Equation 3, the conversion from metre to inch is given by Equation 23. metre is a SI base unit, so no further expansion is necessary.

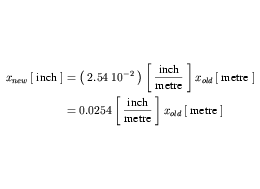(23)

The definition of fahrenheit is in terms of celsius, which is an SI derived unit. The expansion from celsius to kelvin, an SI base unit, is obtained from Section 2.1.1.5 of the SI standard, and is given in Equation 24.

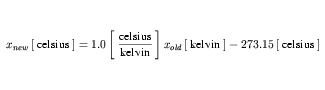(24)

The first step in the expansion of the fahrenheit definition is given in Equation 25.

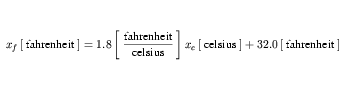(25)

The x_c term can be replaced with the expansion of the celsius definition from Equation 24, as shown in Equation 26.

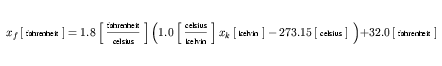(26)

The 1.0 and 273.15 terms can be multiplied by the 1.8. The units on the resulting terms are the products of the units on the operands, as described in Appendix C.3.3, and these can be simplified according to the rules given in Appendix C.3.1. The final expansion of fahrenheit is given in Equation 27

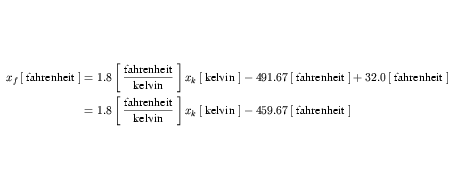(27)

celsius_per_centimetre is the first of the complex units definitions given in Figure 17. The first step in the expansion of this definition is given by Equation 28, which is obtained by substituting the appropriate terms in Equation 4.

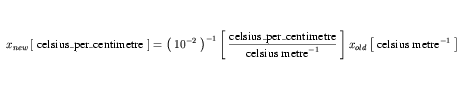(28)

The expansion of the x_old term, which has units that are a product, is not obvious. This term must be expanded to continue. metre is an SI base unit, so need not be expanded. However, celsius is an SI derived unit, the expansion of which is given in Equation 24. Because this expansion is to be substituted into a complex units definition, the offset term is dropped. The next step in the expansion makes use of the modified celsius definition in Equation 29 and the identity in Equation 30.

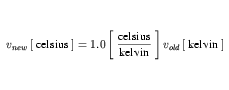(29)

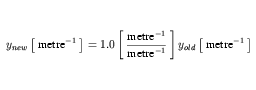(30)

The result of multiplying Equation 30 and Equation 29 is given in Equation 31.

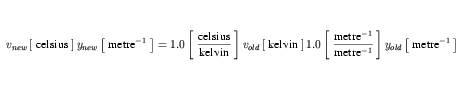(31)

The v_new and y_new variables can be multiplied together to produce a new unknown z_new which has units which are the product of the units on v_new and y_new. Similarly z_old is the product of v_old and y_old. The result is given in Equation 32, where the scale factors have also been multiplied.

(32)

z_new from Equation 32 can be substituted in place of Equation 28, and the result simplified to give the complete expansion of celsius_per_centimetre shown in Equation 33.

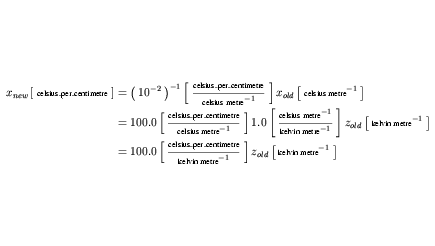(33)

The definition of fahrenheit_per_inch can be handled in the same way. The first step in the expansion is given by Equation 34.

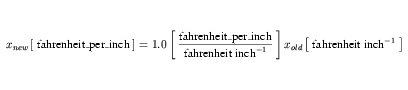(34)

The expansion of x_old requires the removal of the offset from the expansion of fahrenheit from Equation 27 and the inversion of the expansion of inch from Equation 23. These are given in Equation 35 and Equation 36, respectively.

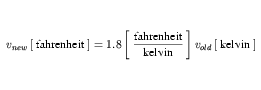(35)

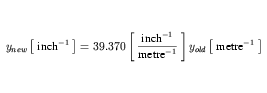(36)

Multiplying Equation 35 and Equation 36 and simplifying yields Equation 37.

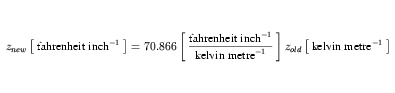(37)

z_new from Equation 37 can be substituted into Equation 34 in place of x_old and the result simplified to give the complete expansion of fahrenheit_per_inch in Equation 38.

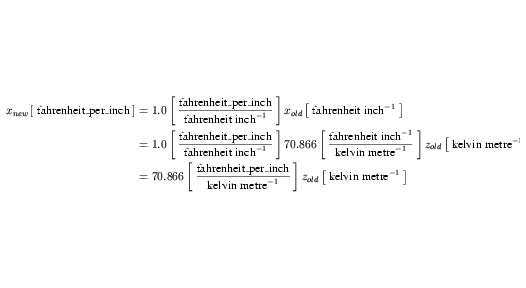(38)

The first step in the expansion of pH_per_celsius is given in Equation 39.

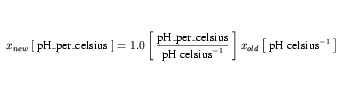(39)

When user-defined base units are referenced in a simple or complex units definition, they are treated in the same way as SI base units, and not expanded. The final expansion into a combination of user-defined and SI base units is given in Equation 40.

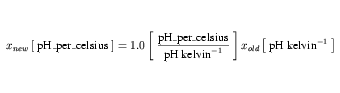(40)

C.4.3  Conversion between units definitions

In this section, the algorithm defined in Appendix C.3.5 for converting a variable's value from one set of units to another is presented with respect to a practical example. Figure 18 contains part of a CellML model definition, consisting of two components and one connection. The legacy_imperial component defines a variable x with units of fahrenheit_per_inch. The modern_si component defines a variable y with units of celsius_per_centimetre. A connection between the two components maps x to y.

<component name="legacy_imperial">
  <variable name="x" public_interface="out" units="fahrenheit_per_inch" />
</component>

<component name="modern_si">
  <variable name="y" public_interface="in" units="celsius_per_centimetre" />
</component>

<connection>
  <map_components component_1="legacy_imperial" component_2="modern_si" />
  <map_variables variable_1="x" variable_2="y" />
</connection>

Figure 18 In this model fragment, a connection maps a variable x with units of fahrenheit_per_inch to a variable y with units of celsius_per_centimetre.

The CellML definitions of both fahrenheit_per_inch and celsius_per_centimetre are given in Figure 17. It was shown how to obtain expressions that relate each of these units definitions to the SI base units in Appendix C.4.2. These expressions are reproduced in Equation 41 and Equation 42, respectively.

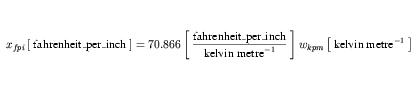(41)

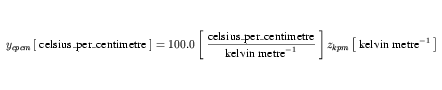(42)

The value of x is transferred to the variable y in the mapping. Therefore an equation expressing celsius_per_centimetre in terms of fahrenheit_per_inch is needed. This can be obtained by rearranging Equation 41 for w_kpm, substituting the resulting expression in place of z_kpm in Equation 42, and simplifying the result according to the rules defined in Appendix C.3.1. This gives the expression in Equation 43.

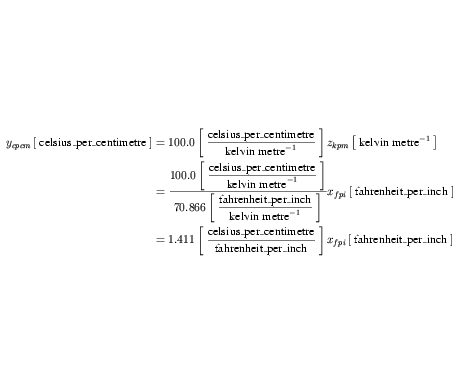(43)

C.4.4  Equation dimension checking

In this section, the algorithm defined in Appendix C.3.6 for checking that an equation has consistent units is presented with respect to a practical example. Figure 19 contains the definition of a CellML component sodium_channel_m_gate. This component defines three sets of units (per_millisecond, millivolt, and per_millivolt), two variables (V and alpha_m) and an equation that calculates the value of alpha_m.

<component name="sodium_channel_m_gate">
  <units name="per_millisecond">
    <unit prefix="milli" units="second" exponent="-1" />
  </units>
  <units name="millivolt">
    <unit prefix="milli" units="volt" />
  </units>
  <units name="per_millivolt">
    <unit prefix="milli" units="volt" exponent="-1" />
  </units>

  <variable name="V" units="millivolt" />
  <variable name="alpha_m" units="per_millisecond" />

  <math xmlns="http://www.w3.org/1998/Math/MathML">
    <apply><eq />
      <ci> alpha_m </ci>
      <apply><times />
        <cn cellml:units="per_millisecond"> 1.0 </cn>
        <apply><divide />
          <apply><times />
            <cn cellml:units="per_millivolt"> 0.1 </cn>
            <apply><plus />
              <ci> V </ci>
              <cn cellml:units="millivolt"> 25.0 </cn>
            </apply>
          </apply>
          <apply><minus />
            <apply><exp />
              <apply><times />
                <cn cellml:units="per_millivolt"> 0.1 </cn>
                <apply><plus />
                  <ci> V </ci>
                  <cn cellml:units="millivolt"> 25.0 </cn>
                </apply>
              </apply>
            </apply>
            <cn cellml:units="dimensionless"> 1.0 </cn>
          </apply>
        </apply>
      </apply>
    </apply>
  </math>
</component>

Figure 19 Parts of the CellML definition of the Hodgkin Huxley squid axon model. The sodium_channel_m_gate component defines three sets of units, two variables V and alpha_m, and the calculation of alpha_m.

Equation 44 gives the equation in Figure 19, where units have been omitted. Equation 45 gives the same equation, with the units associated with each number and variable are included. The first 1.0 in the equation is included specifically for units consistency. It would be possible to associate more complex units with the 0.1 in the numerator of the equation, but this would not accurately reflect the intent of the original model authors. CellML processing software is free to find this and similar terms that do not affect the mathematics and ignore them when interpreting the equation.

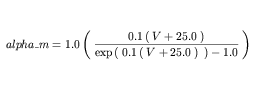(44)

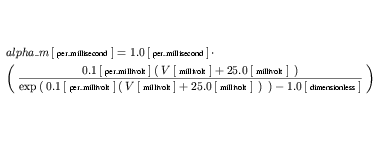(45)

The first step in the algorithm proposed in Appendix C.3.6 for verifying that a given equation has consistent dimensions is to convert the equation into a tree of equation parts. Equation 45 can be broken up into the tree shown in Figure 20.

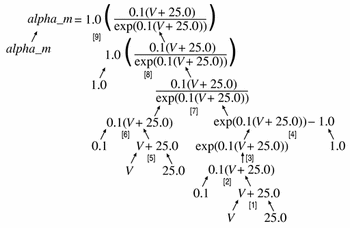
Figure 20 The tree form of Equation 45, in which each non-leaf node is obtained by the application of a single operator to its children. Each operator is represented by a number in square brackets. The effect of each operator is discussed in the text.

At each branch in the tree, a single operator is applied to the child nodes, combining them into a larger parent equation part. Each equation part in the tree has units associated with it. In the case of leaf nodes, these units are obtained from the MathML equation definition. Parent nodes have units defined by the operator and the units on their child nodes, as described in Appendix C.3.3. Dimension checking begins at the leaf nodes, which are recursively removed as the units are evaluated for their parent nodes, which in turn become leaf nodes, as described in Appendix C.3.6.

In the equation tree diagram in Figure 20, the application of each operator to a set of child nodes is denoted by a number in square brackets, where the number reflects the order in which the operations are processed. These operations are discussed below.

1. The <plus> operator combines the variable "V" and the number "25.0" that occur in the denominator of the fraction in Equation 45. The <plus> operator requires all of its operands to be dimensionally equivalent, as described in Appendix C.2.2. The resulting equation part will have the same units as the operands. Both "V" and "25.0" have units of millivolt, and so the parent equation part "V + 25.0" also has units of millivolt.
2. The <times> operator (which is not explicitly rendered in Equation 45) multiplies the "V + 25.0" term that is the result of the first operation by the number "0.1" which has units of per_millivolt. The <times> operator can be applied to any operands, independent of their units, and the resulting equation part has units that are the product of the units on the operands. In this case, the resultant "0.1(V + 25.0)" term has units that are the product of millivolt and per_millivolt, which simplifies to dimensionless (as described in Appendix C.3.1).
3. The <exp> operator is a unary arithmetic operator and its operand must have units of dimensionless. The result of applying the operator, in this case "exp(0.1(V + 25.0))", also has units of dimensionless.
4. The <minus> operator subtracts the number "1.0", which has units of dimensionless, from the term resulting from operation 3. The <minus> operator requires both its operands to have the same units and the result assumes those units.
5. The <plus> operator is applied to the variable "V" and the number "25.0" from the numerator of the fraction in Equation 45. Units are handled as in operation 1.
6. Exactly as in operation 2, where the operands are now in the numerator of the fraction in Equation 45.
7. The <divide> operator is applied to the results of operations 6 and 4, which both have units of dimensionless. The <divide> operator can be applied to any operands, independent of their units, and the result has the quotient of the units on the operands. In this case, the resulting fraction has units of dimensionless.
8. The <times> operator is applied to the number "1.0", which has units of per_millisecond and the result of operation 7, which has units of dimensionless. The resulting term has units of per_millisecond.
9. Finally, the <equals> operator is applied to the variable "alpha_m" and the term resulting from operation 8. The <equals> operator requires that its operands have dimensionally equivalent units.

D  Changes

D.1  Changes between 2 March 2001 Draft and the 18 May 2001 Final Draft

• Language Syntax Changes
  • CellML Identifiers — The definition of a CellML identifier was changed to be consistent with the Systems Biology Markup Language (SBML) specification.
  • Namespaces — It was decided to base the CellML namespaces on a version number rather than a date. The CellML specification does not define the metadata namespaces now. For more detailed information see the meeting minutes from 7 May 2001
  • Connections — The syntax used to pass the values of variables between components was completely revised. The new scheme has more meaningful element and attribute names, is self-consistent, and is more concise. For more detailed information see the meeting minutes from 13 March 2001 and 21 March 2001.
  • Mathematics — The rules regarding the use of MathML in a CellML document were overhauled, and a number of recommendations were added. In particular a subset of the MathML content markup elements was defined and discussion of scripting functionality was moved to an appendix. See the meeting minutes from 21 March 2001, 2 April 2001, and 5 April 2001for more information.
  • Units — Complete worked examples of units conversion and equation dimension checking were added, and complete algorithms for these processes were added to the appendices. See the meeting minutes from 21 March 2001 for more information.
  • Grouping — The grouping syntax was completely overhauled to allow a complete hierarchy to be specified within a single group. See the meeting minutes from 14 March 2001, and 21 March 2001for more information.
• Editorial Changes
  • Conformance Levels amd Terminology — The idea of two conformance levels was discarded, and instead this specification now consists of rules and recommendations. The conformance section was removed from the introduction and a new terminology section was added which properly defines what is expected of valid CellML documents and CellML-compliant processing software. See the meeting minutes from 22 April 2001 for more information.
  • Syntax Related Changes — Major editorial changes were made to properly document the syntax changes described above.
  • Many minor editorial changes, too numerous to list here, have been made to all sections of the specification.